- November 20, 2024
- Ronen Shekel
- 0
Author: Ronen Shekel
Quantum and classical ghost imaging
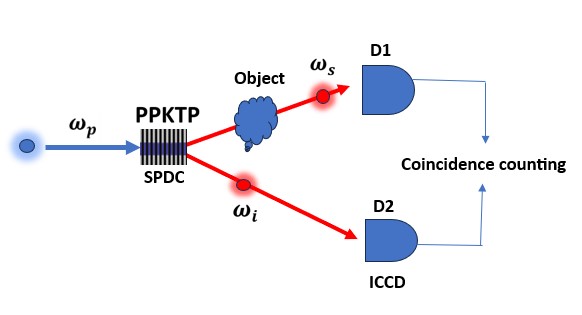
Ghost imaging, one of the first imaging techniques using quantum light, has captivated researchers since its inception in the mid-1990s. The concept of ghost imaging was first demonstrated in 1995 by Pittman et al. [1], using quantum light generated via spontaneous parametric down-conversion (SPDC), a nonlinear optical process that converts a pump photon into two lower-energy entangled photons.
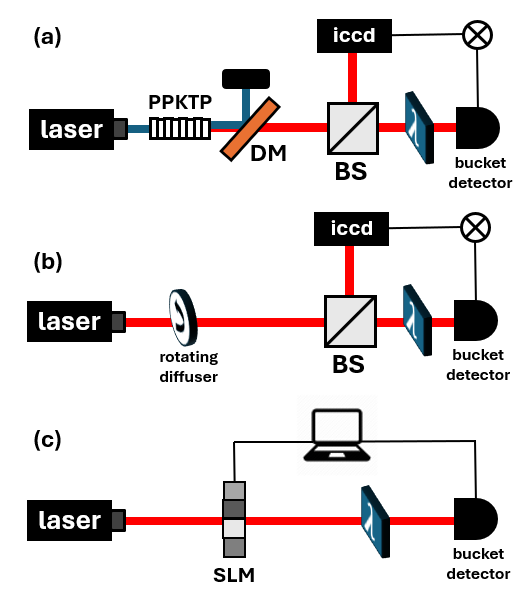
In this experiment (Fig. 1a), the spatially entangled photons are separated, with one photon propagating through an object and being collected using a bucket detector with no spatial resolution, while the idler photon is sent to a multi-pixeled camera. By measuring coincidence events between the bucket detector and the camera, the object is reconstructed, despite the fact that the photons detected by the camera did not directly interact with it! This nonlocal characteristic led to the term “ghost imaging.”
The crux of this technique lies in the spatial correlations of the two photons: areas that are blocked by the object will not reach the bucket detector, so coincidence events will not occur with the corresponding pixels in the camera. But one must remember: correlations do not necessarily imply entanglement! Does quantum entanglement play a critical role in this technique? This was the subject of a debate that lasted several years.
In [2], for instance, theoretical arguments were presented, suggesting that entanglement is intrinsic to ghost imaging. However, in 2002, Bennik et al. [3] demonstrated ghost imaging using two classically correlated beams, randomly deflected at different angles. Others explored similar classical correlations using a rotating diffuser [4], generating correlated pseudo-thermal light (Fig. 1b).
Computational ghost imaging
An important fruit of this debate was that of computational ghost imaging, proposed by Shapiro [5], and demonstrated by Bromberg et al. [6]. In this method, only a single detector is used, and the high-resolution camera is replaced by a computation of the propagating field which is shaped using a spatial light modulator (Fig. 1c). The key point here is that we know everything about the photon propagating to the camera, so we can utilize this knowledge computationally and get rid of the physical camera. The object image is obtained by correlating the intensities measured by the bucket detector with the calculated field at the object plane.
While this computational approach already simplified the experimental setup, researchers soon realized [7] that the number of measurements could be significantly reduced by leveraging modern image processing techniques, particularly those that exploit prior knowledge about the image structure. Remarkably, for most imaging tasks, such information exists: natural images are sparse, that is, they contain many coefficients close to or equal to zero when represented in an appropriate basis. This property of natural images is at the core of modern lossy image compression algorithms, such as JPEG. The field of compressed sensing exploits this sparsity/compressibility to reduce the number of measurements needed for faithful image recovery. Utilizing this technique reduces the number of measurements required for a faithful reconstruction by an order of magnitude.
Current state and future directions
The fact that computational ghost imaging uses only a single detector provides experimental evidence that pseudothermal ghost imaging does not inherently rely on nonlocal quantum correlations. It is now also recognized that the quantum and classical methods produce images of a similar resolution. The main advantage of utilizing quantum light for ghost imaging is found at low light levels, at which the quantum modality exhibits greater visibility and a greater signal-to-noise ratio [8]. This could be especially important when imaging samples that are sensitive to high light levels. Further details comparing the classical and quantum modalities may be found in [9].
Almost 30 years since its first demonstration, many extensions, applications, and modalities of ghost imaging are still being explored. Are you interested in ghost imaging with quantum light? Or perhaps want to explore other use cases for quantum entanglement? Please check out our PPKTP and BBO crystals, used for generating entangled photons, and join the conversation!
[1] Pittman, Todd B., Y. H. Shih, D. V. Strekalov, and Alexander V. Sergienko. “Optical imaging by means of two-photon quantum entanglement.” Physical Review A 52, no. 5 (1995): R3429.
[2] Abouraddy, Ayman F., Bahaa EA Saleh, Alexander V. Sergienko, and Malvin C. Teich. “Role of entanglement in two-photon imaging.” Physical review letters 87, no. 12 (2001): 123602.
[3] Bennink, Ryan S., Sean J. Bentley, and Robert W. Boyd. ““Two-photon” coincidence imaging with a classical source.” Physical review letters 89, no. 11 (2002): 113601.
[4] Valencia, Alejandra, Giuliano Scarcelli, Milena D’Angelo, and Yanhua Shih. “Two-photon imaging with thermal light.” Physical review letters 94, no. 6 (2005): 063601.
[5] Shapiro, Jeffrey H. “Computational ghost imaging.” Physical Review A—Atomic, Molecular, and Optical Physics 78, no. 6 (2008): 061802.
[6] Bromberg, Yaron, Ori Katz, and Yaron Silberberg. “Ghost imaging with a single detector.” Physical Review A—Atomic, Molecular, and Optical Physics 79, no. 5 (2009): 053840.
[7] Katz, Ori, Yaron Bromberg, and Yaron Silberberg. “Compressive ghost imaging.” Applied Physics Letters 95, no. 13 (2009).
[8] Moreau, Paul-Antoine, Ermes Toninelli, Thomas Gregory, and Miles J. Padgett. “Imaging with quantum states of light.” Nature Reviews Physics 1, no. 6 (2019): 367-380.
[9] Erkmen, Baris I., and Jeffrey H. Shapiro. “Ghost imaging: from quantum to classical to computational.” Advances in Optics and Photonics 2, no. 4 (2010): 405-450.
Raicol
Rosh Ha’Ayin 4809162, Israel
